728x90
반응형
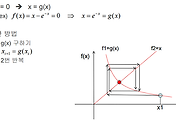
Newton - Raphson 법
● 가장 효율적이고도 주로 사용되는 방법 중의 하나
● 초기값 x1에 대해 점(x1, f(x1))에 접하는 접선을 구하고, 이 접선이 축과 만나는 점이 새로운 근 x2가 됨
Tip. Used APIs
- double log(double x)
#include <stdio.h> #include <math.h> #define THRESHOLD 0.000001 double f(double x) { double ret = 0; ret = log(x + 5.0) + x; return ret; } double f2(double x) { double ret = 0; ret = 1 / (x + 5.0) + 1; return ret; } int main() { double x = 7.0; double x2 = 0; int i = 1; printf("i \t x \t\t f(x)\n"); printf("%d \t %f \t %f\n", i, x, f(x)); while (1) { i++; x2 = x - (f(x) / f2(x)); printf("%d \t %f \t %f\n", i, x2, f(x2)); if (fabs(f(x2)) < 0.000001) break; x = x2; } return 0; }
결과
반응형
'수업 > 수치계산' 카테고리의 다른 글
| [수치계산] 오차&비선형 방정식의 해 - 수렴성 (0) | 2017.06.09 |
|---|---|
| [수치계산] 오차&비선형 방정식의 해 - 할선법 (0) | 2017.06.09 |
| [수치계산] 오차&비선형 방정식의 해 - 고정점 반복법 (0) | 2017.06.09 |
| [수치계산] 오차&비선형 방정식의 해 - 가위치법 (0) | 2017.06.09 |
| [수치계산] 오차&비선형 방정식의 해 - 이분법 (0) | 2017.06.09 |






댓글